Consider the problem of removing edges from a connected, weighted, undirected graph G to form a subgraph such that all the vertices remain connected and the sum of the weights on the remaining edges is as small as possible. Such a problem has numerous applications.

• Road construction: want to connect a set of cities with a minimum amount of road.
• Telecommunications: want to use a minimal length of cable.
• Plumbing: want to use a minimal amount of pipe.

A spanning tree for graph G is a connected subgraph that contains all the vertices in G and is a tree. An algorithm for our problem must obtain a spanning tree of minimum weight. Such a tree is called a minimum spanning tree. A graph can have more than one minimum spanning tree.

A subgraph with minimum weight must be a tree, because if a subgraph were not a tree, it would contain a simple cycle, and we could remove any edge on the cycle, resulting in a connected graph with a smaller weight. It is possible that a graph can have more than one minimum spanning tree.

그래프 G에 대한 신장트리는 G의 모든 정점을 포함한 트리이다. 하나의 그래프에는 여러 신장트리가 존재할 수 있는데, 모든 신장트리가 최소신장트리는 아니다. 이번 알고리즘의 목적은 여러 신장트리 중 가중치 합이 가장 작은 신장트리를 찾는 것이다.

최소의 가중치를 갖는 부분그래프는 반드시 트리이다. 그렇지 않으면 그래프 내에는 순환경로(cycle)가 있을 것이고, 그 순환경로상의 한 이음선을 제거함으로써 더 작은 비용의 신장트리를 만들 수 있다.

Example Determine a minimum spanning tree.

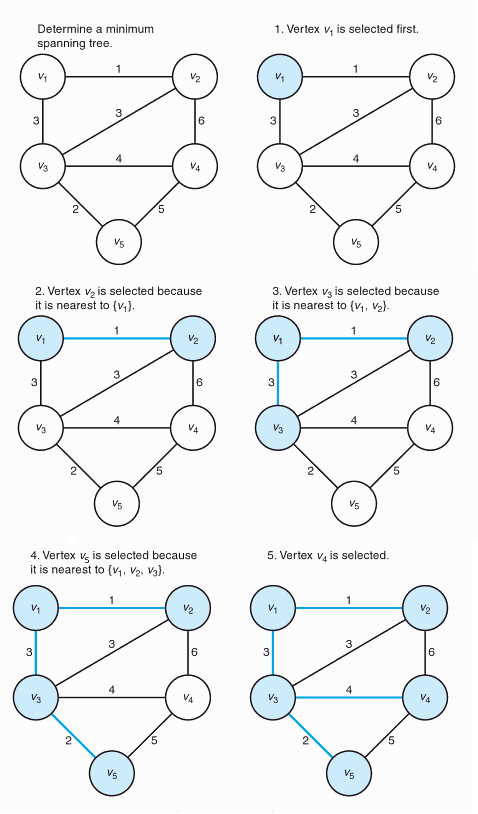
Step 1 시작 정점으로 $v_1$을 선택한다.

Step 2 {$v_1$}에서 가장 가까운 정점인 $v_2$를 추가한다. 여기서 가깝다는 뜻은 이음선의 길이가 가장 작음을 의미한다.

Step 3 {$v_1$, $v_2$}에서 가장 가까운 정점인 $v_3$를 추가한다.

Step 4 {$v_1$, $v_2$, $v_3$}에서 가장 가까운 정점인 $v_5$를 추가한다.

Step 5 {$v_1$, $v_2$, $v_3$, $v_5$}에서 선택되지 않은 가장 작은 이음선의 값은 3이다. 하지만 이 값을 선택하면 순환경로가 생기므로 선택하지 않고, 그 다음 작은 값인 $v_3$과 $v_4$를 잇는 이음선을 선택하면서 마지막 정점인 $v_4$를 추가한다. 이렇게 모든 정점을 포함하게 되면 최소신장트리가 완성된다.

Prim’s Algorithm

Algorithm Design

Prim’s algorithm starts with an empty subset of edges F and a subset of vertices Y initialized to contain an arbitrary vertex. We will initialize Y to {$v_1$}. A vertex nearest to Y is a vertex in V - Y that is connected to a vertex in Y by an edge of minimum weight.

Because at the start Y = {$v_1$}, nearest[i] is initialized to 1 and distance[i] is initialized to the weight on the edge between $v_1$ and $v_i$. As vertices are added to Y, these two arrays are updated to reference the new vertex in Y nearest to each vertex outside of Y. To determine which vertex to add to Y, in each iteration we compute the index for which distance[i] is the smallest. We call this index vnear. The vertex indexed by vnear is added to Y by setting distance[vnear] to −1.

[용어정의]

[프림 알고리즘 초기화 로직]
distance[2]의 값은 W[1][2], distance[3]는 W[1][3], …, distance[k]는 W[1][k] 일 것이다. 왜냐하면 초기화 시점에서 Y에 속한 정점은 시작정점, 즉 $v_1$하나이므로 이를 통해서만 다른 정점으로 갈 수 있기 때문이다. nearest[i]는 시작정점인 $v_1$으로 값을 초기화한다. 즉, nearest[2], nearest[3], …, nearest[k] 모두 1로 초기화 된다. 시작정점을 제외한 다른 모든 정점들에게 가장 가까운 정점을 $v_1$으로 초기화 시키는 것 뿐이다. (해당 정점으로 갈 수 있는 이음선이 없을지라도)

[프림 알고리즘 메인 로직]
시작정점을 포함시키지 않아도 되므로 총 n-1번의 루프 수행과정에서 distance[i]와 nearest[i]값들을 갱신해 나가며 최소신장트리를 완성한다. distance[i]의 값들 중에서 가장 작은 이음선의 값을 찾아 기록한 후, 추가된 정점을 통해 갈 수 있는 이음선의 값이 기존의 값 보다 작다면 distance[i]와 nearest[i] 값을 갱신한다.

이해를 돕기 위해 위의 예제의 $v_2$가 추가되는 과정(Step 2)을 살펴보자. 먼저 $v_2$는 $v_1$에서 가장 가까운(min = 1) 정점이므로 추가가 되고 (vnear = 2), 추후에 다시 고려할 필요가 없기 때문에 distance[vnear = 2]의 값을 -1로 할당한다. $v_2$를 추가함으로써 $v_4$까지 갈 수 있는 이음선이 생기며, 이 값은 6으로 초기값인 ∞보다 작으므로 distance[4], nearest[4]의 값을 갱신한다. 이 과정을 n-1번 반복하게 되며, 그 결과로 최소신장트리를 얻을 수 있다.

Pseudo Code

void prim(int n, const number W[ ][ ], set_of_edges& F)
{
  index i, vnear;
  number min;
  edge e;
  index nearest[2...n];
  number distance[2...n];

  F = "empty";
  for (i = 2; i <= n; ++i)
  {                        // For all vertices, initialize V1 to be the
    nearest[i] = 1;        // nearest vertex in Y and initialize the
    distance[i] = W[1][i]; // distance from Y to be the weight on
  }                        // the edge to V1.

  repeat(n-1 times) // Add all n-1 vertices to Y.
  {       
    min = "infinite";
    for (i = 2; i <= n; i++)       // Check each vertex for      
      if (0 <= distance[i] <= min) // being nearest to Y.
      {   
        min = distance[i];    
        vnear = i;    
      }
    e = edge connecting vertices indexed by vnear and nearest[vnear];
    add e to F;
    distance[vnear] = -1; // Add vertex indexed by vnear to Y.
    for (i = 2; i <= n; i++)
      if (W[i][vnear] < distance[i]) // For each vertex not in Y,
      {                              // update its distance from Y.
        distance[i] = W[i][vnear];  
        nearest[i] = vnear;
      }
  }
}

Source Code

// File: prim.h
#ifndef PRIM_H
#define PRIM_H
#include "graph.h"
using namespace data_structures;

namespace algorithms
{
  struct edge
  {
    std::string vertex[2];
    int weight;
  };
  typedef struct edge edge;
  typedef edge* set_of_edges;

  void prim(int n, const graph g, set_of_edges& F);
  // Problem: Determine a minimum spanning tree.
  // Inputs: integer n >= 2, and a connected, weighted, undirected graph
  // containing n vertices. The graph is represented by a two-dimensional
  // array W, which has both its rows and columns indexed from 1 to n,
  // where W[i][j] is the weight on the edge between the ith vertex and
  // the jth vertex.
  // Outputs: set of edges F in a minimum spanning tree for the graph.

  template <typename Item>
  Item* get_vector_space(const int n)
  // Postcondition: Return the array containing n spaces
  {
    Item* v = new Item[n];
    return (v-1); // offset the pointer
  }
}

#endif

// File: prim.cpp
#include "prim.h"

namespace algorithms
{
  void prim(int n, const graph g, set_of_edges& F)
  {
    int i, vnear;
    int min;
    edge e;
    int* nearest = get_vector_space<int>(n);
    int* distance = get_vector_space<int>(n);

    // For all vertices, initialize V1 to be the nearest vertex in Y
    // and initialize the distance from Y to be the weight on the edge to V1.
    for (i = 2; i <= n; ++i)
    {                           
      nearest[i] = 1;                   
      distance[i] = g.get_edge(1, i);
    }                                    

    int repeat = 0;
    while (repeat < n-1) // Add all n-1 vertices to Y.
    {
      min = graph::INFINITE;
      for (i = 2; i <= n; ++i) // Check each vertex for being nearest to Y
      {
        if (distance[i] >= 0 && distance[i] < min)
        {
          min = distance[i];
          vnear = i;
        }
      }

      // edge connecting vertices index by vnear and nearest[vnear]
      e.vertex[0] = g[nearest[vnear]];         
      e.vertex[1] = g[vnear];
      e.weight = min;
      F[repeat++] = e; // add e to F

      distance[vnear] = -1;
      for (i = 2; i <=n ;++i)
      {
        if (g.get_edge(i, vnear) < distance[i])
        {
          distance[i] = g.get_edge(i, vnear);
          nearest[i] = vnear;
        }
      }
    }
  }
}

#include <iostream>
#include <cstdlib> // Provides EXIT_SUCCESS;
#include <iomanip> // Provides setw
#include "graph.h" // Provides graph
#include "prim.h"  // Provides Prim's algorithm
using namespace std;
using namespace data_structures;
using namespace algorithms;

int main( )
{
  const int GRAPH_SIZE = 5;
  graph example(GRAPH_SIZE);
  example.set_vertex("V1");
  example.set_vertex("V2");
  example.set_vertex("V3");
  example.set_vertex("V4");
  example.set_vertex("V5");
  example.set_edge(1, 2, 1);
  example.set_edge(1, 3, 3);
  example.set_edge(2, 1, 1);
  example.set_edge(2, 3, 3);
  example.set_edge(2, 4, 6);
  example.set_edge(3, 1, 3);
  example.set_edge(3, 2, 3);
  example.set_edge(3, 4, 4);
  example.set_edge(3, 5, 2);
  example.set_edge(4, 2, 6);
  example.set_edge(4, 3, 4);
  example.set_edge(4, 5, 5);
  example.set_edge(5, 3, 2);
  example.set_edge(5, 4, 5);

  //display_graph(example);
  set_of_edges F = new edge[GRAPH_SIZE-1];
  prim(GRAPH_SIZE, example, F);

  cout << "Given a graph, the minimum spanning tree consists of " << endl;
  for (int i = 0; i < GRAPH_SIZE-1; ++i)
  {
    cout << setw(7) << "From" << setw(3) << F[i].vertex[0] << setw(3)
         << "to" << setw(3) << F[i].vertex[1] << ": "
         << F[i].weight << endl;
  }

  return EXIT_SUCCESS;
}

Time Complexity Analysis

Basic operation

• There are two loops, each with n-1 iterations, inside the repeat loop. Executing the instructions inside each of them can be considered to be doing the basic operation once.

Input size

• n, the number of vertices.

Every-Case Time Complexity

• $T(n) = 2(n-1)(n-1) \in \Theta (n^2)$

Optimality Proof

Although greedy algorithms are often easier to develop than dynamic programming algorithms, usually it is more difficult to determine whether or not a greedy algorithm always produces an optimal solution. Recall that for a dynamic programming algorithm we need only show that the principle of optimality applies. For a greedy algorithm we usually need a formal proof. Next we give such a proof for Prim’s algorithm.

프림 알고리즘이 찾아낸 신장트리가 최소신장트리인지 검증해야 한다. 다시 말하자면, 동 알고리즘을 통해 얻은 해답이 최적(optimal)인지를 결정해야 한다. 증명을 위해 보조 정리(Lemma)가 참임을 보이고 이를 이용하여 귀납법으로 프림 알고리즘이 최적의 원칙을 준수하는지 증명한다.

Lemma

Lemma Let G = (V, E) be a connected, weight, undirected graph; let F be a promising subset of E; and let Y be the set of vertices connected by the edges in F. If e is an edge of minimum weight that connects a vertex in Y to a vertex in V - Y, then F U {e} is promising.

G = (V, E)는 연결되고, 가중치가 있는 비방향성 그래프라고 하자. F는 E의 유망한 부분집합이라 하자. Y는 F의 이음선들에 의해 연결된 정점들의 집합이라 하자. 이때 Y에 있는 정점과 V - Y에 있는 정점을 잇는 이음선 중, 그 가중치가 가장 작은 이음선을 e라고 하면, F U {e}는 유망하다.

유망하다는 말은, 비방향성 그래프 G = (V, E)가 주어지고 만약 E의 부분집합인 F에 최소신장트리가 되도록 이음선을 추가할 수 있으면 F는 유망하다(promising)라고 한다.

Proof Because F is promising, there must be some set of edges F’ such that F ⊆ F’ and (V, F’) is a minimum spanning tree.

F가 유망하기 때문에(F에 최소신장트리가 되도록 이음선 추가 가능), F ⊆ F’ 이면서 (V, F’)가 최소신장트리가 되는 이음선의 집합 F’가 반드시 존재한다.

• If e ∈ F’, then F U {e} ⊆ F’, which means F U {e} is promising.

만일 e ∈ F’라면, F U {e} ⊆ F’가 되고, 따라서 F U {e}도 유망하다.

• Otherwise, because (V, F’) is a spanning tree, F’ U {e} must contain exactly one simple cycle and e must be in the cycle. There must be another edge e’ ∈ F’ in the simple cycle that also connects a vertex in Y to one in V - Y. If we remove e’ from F’ U {e}, the simple cycle disappears, which means that we have a spanning tree. Because e is an edge of minimum weight that connects a vertex in Y to on in V - Y, the weight of e must be less than or equal to the weight of e’ (in fact, they must be equal.) So F’ U {e} - {e’} is a minimum spanning tree. Now F U {e} ⊆ F’ U {e} - {e’}, because e’ cannot be in F (recall that edges in F cannot only vertices in Y.) Therefore, F U {e} is promising.

만일 e ∉ F’ 라면, (V, F’)는 이미 신장트리라는 뜻이다. 따라서 F’ U {e}는 정확히 하나의 단순순환경로를 포함해야하고 e는 그 순환경로 내에 있어야 한다. (위의 예제에서는 $v_1$ $\rightarrow$ $v_2$ $\rightarrow$ $v_4$ $\rightarrow$ $v_3$ $\rightarrow$ $v_1$)
Y에 있는 한 정점에서 V - Y에 있는 한 정점을 연결하는 임의의 이음선 e’ ⊆ F’는 그 순환경로 안에 반드시 존재하게 된다.

F’ U {e}에서 e’를 제거하면 단순순환경로는 사라지며 다시 신장트리가 형성된다. e는 Y에 있는 한 정점에서 V - Y에 있는 한 정점을 연결하는 최소가중치 이음선이므로, e의 가중치는 반드시 e’의 가중치 보다 작거나 같다. (실제로 반드시 같게 된다.) 그러면 F’ U {e} - {e’}는 최소신장트리이다.

결론적으로 e’가 F안에 있을 수 없으므로(F안에 있는 이음선들은 Y안에 있는 정점들 만을 연결함을 기억하라) F U {e} ⊆ F’ U {e} - {e’}가 되고, 따라서 F U {e}는 유망하다.

Theorem: Prim’s algorithm always produces a minimum spanning tree.

Proof We use induction to show that the set F is promising after each iteration of the repeat loop.
Induction base Clearly the empty set is promising.
Induction hypothesis Assume that, after a given iteration of the repeat loop, the set of edges so far selected - namely, F is promising.
Induction step We need to show that the set F U {e} is promising, where e is the edge selected in the next iteration. Because the edge e selected in the next iteration is an edge of minimum weight that connects a vertex in Y to one on V - Y, F U {e} is promising, by Lemma. This completes the induction proof.

매번 반복이 수행된 후 E의 부분집합 F에 최소신장트리가 되도록 이음선을 추가할 수 있다는 것을 보이면 된다. (즉, F는 유망하다는 것을 입증한다.)

처음 시작은 공집합이다. 연결되고, 가중치가 있는 비방향성 그래프에서는 항상 최소신장트리가 존재하므로, 공집합 F를 포함하는 최소신장트리가 존재한다. 따라서 공집합이 아닌 F에 대해 F U {e}가 유망하다는 사실만 보이면 된다.

e는 다음 반복에서 선택된 이음선이다. e는 Y에 있는 정점을 V - Y에 있는 정점으로 연결하는 최소가중치를 지닌 이음선이기 때문에, 보조정리에 따라 F U {e}는 유망하다고 할 수 있다. 이것으로 귀납 증명이 완료된다.